El método ABN. Una alternativa para la enseñanza de las matemáticas

Introducción

Las matemáticas constituyen un aspecto fundamental en el desarrollo del niño/a. Por ello, resulta imprescindible trabajar en esta etapa las capacidades vinculadas al desarrollo lógico-matemático, pues son las que permitirán al niño/a conocer la realidad y los objetos que la componen, establecer relaciones entre ellos, descubrir sus características, organizarlos, compararlos, agruparlos, y de este modo, ir ampliando su concepción del mundo y de sí mismo.

Desde muy pequeños, entramos en contacto con el mundo de los números y las matemáticas. Por ello, debemos desarrollar una actitud positiva y motivadora hacia los contenidos matemáticos construyendo las bases necesarias para el posterior desarrollo de conceptos matemáticos más complejos. En este sentido, debemos partir de una estimulación temprana de las matemáticas desde la etapa de Educación Infantil. Así, autores como Román y Murillo (2010) confirman que los niños/as que han asistido a esta etapa están mejor preparados para afrontar etapas educativas posteriores, siendo la asistencia a la Educación Infantil un factor relevante en su rendimiento académico (Santín y Sicilia, 2015).

Sin embargo, es una realidad que en etapas educativas posteriores se viene observando un fracaso en el área de las matemáticas. Por este motivo, el interés de los investigadores se ha centrado en investigar el desempeño matemático para detectar las dificultades de aprendizaje en matemáticas (Butterworth, Varma, y Laurillard, 2011) y se han propuesto nuevos métodos de intervención para su mejora (Aragón, Aguilar, Navarro, y Araujo, 2015; Martínez y Sánchez, 2013). Cuando hablamos de alumnado que manifiesta dificultades de aprendizaje de las matemáticas nos encontramos con estudiantes que no son capaces de desenvolverse adecuadamente a la hora de resolver problemas o cálculos y que sus habilidades matemáticas no se corresponden con las que muestran otros estudiantes de su misma edad (Fletcher, Lyon, Fuchs, y Barnes, 2007; Fuchs et al., 2008). A partir de los resultados obtenidos en un estudio reciente podemos confirmar que las dificultades de aprendizaje surgen antes de la educación de tipo formal (Aunio, Heiskari, Van Luit y Vuorio, 2015).

El método ABN

Las siglas ABN significan: Método de Cálculo Abierto basado en Números. Su autor es Jaime Martínez Montero, maestro y doctor en Filosofía y Ciencias de la Educación, que explica: “La idea de crearlo es más el resultado de toda una vida profesional en la que se ha trabajado con especial intensidad la didáctica de las matemáticas, que algo que se le ocurre a uno de repente”. En este sentido, Martínez Montero ha escrito varios libros relacionados con el tema, que son una interesante fuente de consulta para los docentes como: “Una nueva didáctica del cálculo para el siglo XXI” y “Competencias básicas en matemáticas. Una nueva práctica”. Su aplicación se inició por primera vez en un aula de 1º de Primaria del CEIP Andalucía (Cádiz, curso 2008-2009). Se trata de un método natural, que se relaciona con la forma espontánea e intuitiva que tiene el cerebro para procesar los cálculos y tratar las realidades numéricas. Por ello, la metodología en la escuela debe aprovechar las experiencias informales que tienen los niños/as, en lugar de partir de cero. Permite trabajar con cantidades concretas, manipularlas, descubrir sus reglas, construir los números y las relaciones que se establecen entre ellos, permitiendo a los niños y niñas aplicar sus propias estrategias, al contrario que con el método tradicional, que trata al número como algo estático, determinado y cerrado (Martínez y Sánchez, 2011).

Significado del método ABN

En las siglas que componen su nombre (ABN) podemos encontrar dos de sus características fundamentales, teniendo en cuenta a varios autores como García y Quirell (2017), Díaz, Torres y Lozano (2017) y Brancho (2013):

La «A» significa «ABIERTOS», ya que plantea distintas formas de resolver un mismo problema o situación, es decir, cada alumno puede elegir libremente la manera en la que quiere resolverlo, pero todos van a llegar al mismo resultado. En contraposición a los métodos tradicionales que son cerrados, es decir, con una única forma de realizarlos, a través de una serie de instrucciones que los alumnos/as llevan a cabo de manera memorística y automática, sin entender en qué se basan.
«BN» hace referencia a «BASADOS EN NÚMEROS» y no en cifras como los algoritmos tradicionales, es decir, dónde las unidades, las decenas, las centenas… se componen y se descomponen libremente sin aplicar una determinada regla o criterio para su resolución final. En cambio, en el método tradicional, las cuentas se realizan sobre las cifras por separado sin tener en cuenta el lugar que ocupan, ya sea en las decenas, unidades, centenas, etc., y se les aplica el mismo tratamiento, es decir, el proceso de resolución va a ser siempre el mismo para cada cifra, con lo cual se pierde el sentido que tienen esas cantidades. (párr. x)

Objetivo, finalidad y principios del método ABN

El objetivo principal de esta metodología es el desarrollo de la lógica y el razonamiento matemático a través de instrumentos manipulativos, lo que conlleva el aumento de la motivación y la mejora de la atención del alumno/a.

Por ello, la finalidad del cálculo ABN según García y Quirell (2017) es la siguiente: “que el niño entienda el número, las combinaciones y trasformaciones que puede hacer con ellos. No se trata de aprender reglas ni trucos para calcular sino entender qué es lo que están haciendo y por qué” (p. 7). También señalan que: “su fundamento principal es el trabajo con números “completos”, con su “significado” y no en “cifras descontextualizadas” (p. 7).

Por otro lado, los principios en los que se base el método son los siguientes (Martínez, 2011):

– Principio de igualdad: “el ser humano nace muy bien dotado para el aprendizaje matemático. Es capaz de desarrollar notables destrezas incluso en ausencia de instrucción” (p. 98). Hay alumnos/as que tienen más facilidad para aprender que otros, pero con las ayudas necesarias todo el mundo puede lograr una competencia matemática aceptable.

– Principio de la experiencia: “la matemática es una materia muy abstracta, y los niños y niñas de la escuela primaria deben abstraer un conjunto de conceptos cuando su pensamiento se encuentra en la fase de operaciones concretas” (p. 98). No se puede eliminar la experiencia manipulativa con los objetos o acciones por experiencias verbales. Por ello, el alumnado debe ser el propio constructor de su aprendizaje, tiene que experimentar, probar, no sirve que vea hacerlo a otra persona.

– Principio del empleo de números completos: es uno de los aspectos característicos de este método.

“Es un principio que marca el punto de ruptura con la metodología tradicional. El alumno manipula, opera, calcula y estima con números completos, sin divisiones artificiales que le llevan a trabajar exclusivamente con cifras sueltas. Cuando el tamaño o estructura del número hagan que sea muy compleja su utilización, el sujeto lo divide en números completos más pequeños, pero nunca en unidades sin sentido”
(p. 98)

– Principio de la transparencia: en este caso, hay que diferenciar entre dos puntos de vista diferentes. Por un lado “en el aprendizaje de los contenidos matemáticos no se ocultan los pasos y procesos con que se construyen los mismos. Todos los algoritmos ABN reflejan con absoluta fidelidad los pasos intermedios que se realizan en la construcción del resultado” (p. 99), por otro lado, plantea que “los materiales y recursos simbólicos que se empleen reflejen de la forma más fiel posible la realidad que toman como referencia. En este caso los materiales utilizados en el método cumplen este requisito” (p. 99).

– Principio de la adaptación al ritmo individual de cada sujeto: no se puede pretender que todos los alumnos/as realicen las mismas tareas y en el mismo tiempo. Por eso, “la estructura de los algoritmos ABN es muy flexible, y hace posible la adaptación al ritmo individual de cada uno, permitiendo los desdobles y facilitando cálculos que en los formatos tradicionales son, sencillamente, imposibles” (p. 99).

– Principio del autoaprendizaje y del autocontrol: esto se consigue gracias a la particular estructura que compone el método, como menciona Martínez (2011):

El poder desdoblar o agrupar los diversos cálculos, el manejo simultáneo de la totalidad de la estructura aditiva o multiplicativa de que se trate, el control de todos los pasos intermedios, abre las posibilidades de integrar y acortar los procesos intermedios, así como el que sea el propio sujeto el que verifique la exactitud de lo que hace.
(p. 99)

Comparación de las características principales del método tradicional con las del método ABN

Una vez realizada una breve aproximación teórica sobre la metodología ABN, vamos a comparar sus características principales con las del método tradicional o método cerrado basado en cifras (CBC):

El método tradicional es cerrado, basado en cifras y se aprende a realizar las operaciones de forma mecánica sin entender los conceptos. Se basa en el ábaco, comienza el cálculo por la derecha, de manera contraria a cómo funciona nuestro procesamiento cerebral. Se trata de un sistema basado en reglas para memorizar. Parte de situaciones ficticias, plasmadas en los libros y cuadernillos. Además, se basa en un sistema de cálculo memorístico, posicional, ciego e inflexible; sin sentido para el alumno. Las operaciones básicas siempre llevan llevadas. No saca partido a las capacidades del alumnado en su periodo sensible. El formato de las operaciones es opaco. La resolución de las operaciones básicas se lleva acabo siguiendo una serie de reglas y pasos posibles de adaptar a la individualidad del alumnado, “se hace así” y no hay más opciones. Impide la estimación: ya que desde la derecha es imposible saber qué cantidad vamos a obtener hasta que no lleguemos al final. Se muestra más dificultad a la hora de resolver problemas y se suelen obtener bajos rendimientos en las pruebas escritas. Suele ser una de las asignaturas que menos gusta en el ámbito escolar y que más difícil suele resultar.

El método ABN es un método de algoritmos abiertos. Basado en el sistema de numeración decimal o base 10. El cálculo es de izquierda a derecha. Supone un cambio de paradigma para los docentes, el alumnado y las familias. Utiliza situaciones cercanas relacionadas con la experiencia del niño/a. Sustituye el cálculo posicional por un cálculo abierto. Elimina las temidas “llevadas”. Busca potenciar las capacidades del alumnado en su periodo sensible. El formato de las operaciones es transparente, de números completos, por lo que la lectura y comprensión de lo que se hace resulta fácil. Además, permite seguir los pasos que el alumno va dando mientras resuelve la actividad, lo que permite detectar, si se produce algún fallo, el punto exacto en el que se ha producido. El alumno adapta las operaciones a su nivel de dominio en el cálculo y no es él quien se adapta a la operación. El niño/a elige cómo hacerlo para tener éxito. Mejora la estimación y el cálculo mental ya que se operan primero las cantidades mayores y luego las menores. Se aumenta notablemente la capacidad de resolución de problemas. Suele dar un aumento de la motivación y actitud positiva frente a esta materia.

Dificultades de la materia de las matemáticas

Es muy común a la hora de hablar de matemáticas, que surja en nosotros un recuerdo negativo e incluso desagradable. Por otro lado, como exponen Martínez y Sánchez (2011), si hacemos referencia a los docentes, “tienen una sensación de frustración permanente: su enseñanza es muy desagradecida, porque requiere grandes dosis de esfuerzo para escasos logros de aprendizaje” (p. 25). Además, hay muchos estudios como el Informe Pisa (2018), en el que nos muestra que las matemáticas es una de las asignaturas que más se suspenden durante la vida escolar del alumno.

El profesor Servais (1980) (citado por Martínez y Sánchez, 2011) aportó una serie de razones por las que el aprendizaje de las matemáticas puede resultar complejo:

– Nivel de abstracción: “la matemática es la más abstracta de las actividades mentales, la más virtual respecto a lo concreto” (p. 25). Pues a diferencia de lo que ocurre con otras áreas de conocimiento, no existen en la realidad, teniendo que recurrir a la representación o simbolización para poder trabajar con ellas.

– Carácter acumulativo: “la matemática es la rama más acumulativa que existe. Cualquier estadio de dominio que se alcance requiere tener activos y sabidos absolutamente todos los estadios anteriores” (p. 25).

– Necesidad de un maestro: “se pueden dar casos de autoaprendizaje, pero son muy raros y se presentan en sujetos de gran capacidad intelectual” (p. 26).

– El vivir diario aporta poco material para el estudio de la matemática: “la mayor parte del aprendizaje matemático del alumno es virtual, de ensayo, sin aplicación, carente de contenido concreto” (p. 26).

– Elevado nivel de concreción:“o se sabe o no se sabe […] Tampoco se puede aportar un enfoque propio o realizar una aportación personal” (pp. 26-27).

Además de estos aspectos, y tal y como señala Ramos (2005):

Muchas de las dificultades en las nociones lógico matemáticas vienen ocasionadas por la confluencia de distintas destrezas cognitivas implicadas en su aprendizaje, como la memoria de trabajo, dificultades para mantener la atención numérica, atención, lectoescritura…, pero, al margen de estos aspectos, la dificultad tiene que ver con la forma de presentarla y las estrategias de enseñanza que se aplican. (p. x)

En este sentido, el enfoque tradicional que se da actualmente en la mayoría de las aulas, no permite al niño/a inventar ni experimentar y los conocimientos que con él se adquieren son fijos y cerrados. Como afirma Le Lionnais (1976) (citado por Díaz, Torres y Lozano, 2017), las matemáticas “constituyen una de las formas más reveladoras y sorprendentes del pensamiento humano. Por ello, hacer matemáticas en cualquier nivel, es o debería ser, siempre una tarea humana apasionante, enriquecedora, única” (p. 1).

Teniendo en cuenta estos aspectos, Martínez y Sánchez (2011) hacen hincapié en que la etapa de Educación Infantil es la mejor para el aprendizaje de esta materia ya que:

Como señala la psicología evolutiva, durante su tránsito por esta fase de la escolarización el niño experimenta el mayor crecimiento cognitivo de todas las etapas escolares. Es, por tanto, un periodo para ser aprovechado especialmente, porque más adelante no se volverán a dar las condiciones tan favorables que se presentan en los tempranos años del recorrido escolar (p. 30).

Por todo esto, una alternativa que se opone a las enseñanzas del método tradicional y que tiene en cuenta la importancia de las matemáticas en la etapa de Educación Infantil como base para poder adquirir el complejo sistema de las matemáticas (Díaz, Torres y Lozano, 2017) es el método ABN que se basa en un enfoque intuicionista.

Ventajas del método ABN

Según Martínez (2010), el método de algoritmos ABN sigue una metodología novedosa y entre las ventajas que señala sobre este método destacan las siguientes:

La metodología ABN supone un cambio cualitativo en la cantidad y en la calidad de los logros matemáticos del alumnado.
Los niños/as aprenden más rápido y mejor.
Mejora la capacidad de estimación, el cálculo mental y la capacidad de resolución de problemas.
Cada niño/a hace las operaciones según su propia capacidad.
Desaparecen ciertas dificultades y trabas con las llevadas, colocación de las cifras, el orden de los términos, etc.
El niño/a entiende lo que hace, le da sentido y verbaliza en todo momento los procesos que está siguiendo.
Hay una mejora efectiva de la motivación y un cambio muy favorable en la actitud de los niños ante la matemática, les gusta y las encuentran divertidas. (p. x).

Por otro lado, también tiene una serie de ventajas para el docente, Martínez (2010): La satisfacción de enseñar los procesos de razonamiento.

«La satisfacción al adaptarse a cada alumno/a según su ritmo de aprendizaje.Reduce la frustración docente y el estrés al enseñar a pensar, abstraer, razonar, etc.”
(p. x).

En esta línea, encontramos varios artículos y páginas web, en las que observamos los beneficios que esta metodología aporta en las aulas. Así, por ejemplo, Quicios (2017) expone:

Mejora la capacidad de cálculo que se basa en el dominio de la numeración sin la necesidad de trucos añadidos.
Es un método que se adapta al alumno. No hay solo una manera de calcular por lo que el niño puede elegir el camino que seguir al resolver los problemas y los cálculos.
Ayuda al desarrollo la de seguridad en sí mismo. Este método ayuda a perder el miedo a enfrentarse a las operaciones.
Hace a los niños más creativos. El carácter abierto del método hace que incluso se puedan crear nuevas operaciones que simplifiquen el procedimiento.
Aporta calidad al aprendizaje. Gracias a todo lo anterior este método permite subir el nivel y adelantar el aprendizaje natural de contenidos de posteriores etapas.
Aporta a la asignatura de matemáticas carácter lúdico. Es un juego donde se proponen retos personales que aumentan la motivación hacia nuevos aprendizajes.
Aumenta la satisfacción tanto de los profesores como de los padres. (p. x).

Aplicación del método ABN

El método ABN de numeración, cálculo y resolución de problemas se puede aplicar en los niveles de Infantil, Primaria e incluso Secundaria (actualmente hasta segundo de la ESO), pero para que los resultados sean más satisfactorios es aconsejable que se inicie en la etapa de Educación Infantil, concretamente en el nivel de 3 años, y que después, poco a poco vaya implantándose en los cursos superiores. En este sentido, nos podemos preguntar ¿por qué debe iniciarse en la etapa de Educación Infantil? Según Martínez y Sánchez (2011), “la Educación Infantil es el periodo de la vida del ser humano en que se experimenta mayor crecimiento cognitivo” (p. x). Además, en esta etapa educativa el niño/a es absolutamente transparente en su conducta en el aula, acepta como en ningún otro momento escolar la influencia del maestro/a, nunca habrá tantas posibilidades de unificar lo que se hace en el colegio con lo que se hace fuera de él, y la colaboración y la atención con los padres es especialmente cercana a la escuela (Martínez y Sánchez, 2011).

¿Cómo aplicar el método ABN en un aula de infantil?

A la hora de introducir el método ABN hay una serie de fases que debemos tener en cuenta:

1ª Fase: manipular, tocar, comprobar.

2ª Fase: gráfica. Va introduciendo signos numéricos y fichas.

3ª Fase: abstracta. No necesita materiales para resolver tareas matemáticas

También Martínez (2011), nos da algunos consejos que nos pueden ayudar antes de implantar el método ABN en nuestras aulas:

No correr, podemos avanzar cuando hayan superado lo que estamos trabajando.
La base del método es la numeración. Hay que dominarla para empezar con el cálculo.
Otro de los pilares es la manipulación. La abstracción al papel es el final del proceso.
Para el trabajo con operaciones, los palillos son una herramienta manipulativa básica.
Jamás evaluar al alumno ABN con los niveles que son capaces de alcanzar, si no conforme a los contenidos mínimos que establece el currículum. (p. x)

Como ya hemos mencionado anteriormente, la etapa de Educación Infantil asienta las bases de la metodología ABN y es necesario invertir bastante tiempo en ello. En esta etapa el niño pasa por diferentes fases a la hora de aprender los números que debe ir afianzando para pasar a los siguientes niveles que forman parte de la etapa de Primaria. Para desarrollar el sentido numérico en los alumnos, debemos estructurar nuestro trabajo en tres grandes ejes:

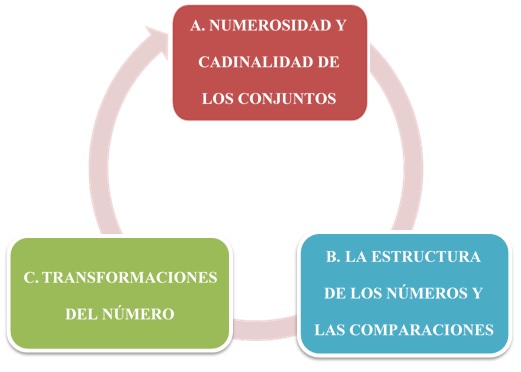
*Figura 2.* Bloques para trabajar el ABN. Fuente: Martínez y Sánchez (2011).

Estos bloques deben presentarse secuencialmente, ya que van de menor a mayor dificultad de aprendizaje, por lo tanto, empezaremos por el bloque uno hasta llegar al bloque tres.

¿Quién puede aplicar este método?

Tanto los docentes como las familias pueden utilizar esta innovadora metodología. Lo fundamental para aplicarla adecuadamente sería la realización de algún curso de formación en ABN. También es necesario contar con la cooperación de todo el equipo docente del centro para poder seguir la secuencia del método ABN desde educación infantil hasta la educación primaria. Por este motivo, debemos mantener una estrecha colaboración con las familias con las cuales llevaremos a cabo un continuo intercambio de información y pautas de actuación. Podemos organizar reuniones, talleres…, para explicarles en qué consiste la metodología ABN y qué actividades pueden realizar en casa para reforzar los contenidos con sus hijos/as.

¿Qué materiales necesito para aplicarlo en mi aula?

Los materiales que podemos utilizar con este método son muy amplios y fáciles de conseguir. Podemos incluso elaborarlos nosotros mismos a partir de materiales de desecho, por lo que no suponen un gasto económico elevado. Sin embargo, hay una serie de materiales básicos que vamos a necesitar para trabajar esta metodología y que son:

Alfombra con los números del 0 al 10 de goma eva. Preferiblemente desmontable, ayuda a poder interiorizar el orden de los números: si ando hacia delante crece, si retrocedo, decrece. El movimiento del salto, le ayudará a aprender este concepto.
Recta numérica en horizontal.
Tabla del 100 y maletín de números. Lo ideal es que sea desmontable, es decir, que podamos voltear los números, o quitarlos para descubrir el que falta.
Policubos. Se trata de un recurso polivalente y desmontable que favorece la composición y la descomposición de los números.
Depresores/palillos. Para trabajar las decenas con el ABN, necesitamos palillos o depresores que nos van a permitir hacer las decenas y las unidades. Indispensable tener una caja llena de depresores en el aula y gomas elásticas para atar las decenas.
Tarjetas con las grafías de los números. Debemos tener más de una tarjeta de cada número, decenas completas y signos de sumar, restar e igual.
Platos de plástico. Para realizar equivalencias o repartos, son fundamentales.
Dados. Pueden de ser de todos los tamaños, formas, colores… son muy motivadores y prácticos para trabajar ABN.
Tarjetas de las manos.
Cubiteras o hueveras. muy necesarias para situaciones de comparación o igualación entre otras.
Cualquier material que sirva para contar: pinzas, botones, tapones, coches, lápices, ceras, rotuladores…

En resumen, cualquier material sirve para trabajar el método ABN y no es necesario disponer una gran cantidad de recursos para poder llevarlo a cabo en nuestras aulas. Cada maestro/a puede elegir y crear el material que mejor responda a su creatividad e iniciativa.

Conclusión

En definitiva, se trata de un método muy novedoso que ofrece muchas posibilidades al profesorado. En muchas ocasiones el miedo hacia lo desconocido nos hace quedarnos en lo que hemos utilizado toda la vida, pero debemos mirar hacia adelante y no olvidar que nuestra meta educativa es el desarrollo integral del niño/a, y si este método nos permite desarrollar en nuestros alumnos/as la competencia matemática de una forma sencilla y lúdica, debemos adaptarnos y ampliar nuestro conocimiento hacia otras formas de enseñanza más innovadoras y completamente válidas.

Por ello, sería muy apropiado hacer llegar esta metodología a todos los docentes y centros educativos, para darla a conocer y que de esta manera puedan tener en cuenta, desde el principio de curso, otra manera distinta de enseñar matemáticas, hasta el punto de poder implementarla poco a poco en los colegios, tras haber observado que se obtienen mejores resultados que con el método tradicional y que contribuye a la satisfacción personal de alumnos, padres y profesorado.

Carolina Del Rey Gómez

Referencias bibliográficas

Aragón, E., Aguilar, M., Navarro, J. I., y Araujo, A. (2015). Efectos de la aplicación de un programa de entrenamiento específico para el aprendizaje matemático temprano en educación infantil. Revista Española de Pedagogía, 260, 99-113.

Aunio, P., Heiskari, P., Van Luit, J. E., y Vuorio, J. (2015). The development of early numeracy skills in kindergarten in low, average and high performance groups. Journal of Early Childhood Research, 13(1), 3-16. doi: 10.1177/1476718X14538722

Bracho-López, R. (2013). Menos reglas y más sentido: alternativas metodológicas a los algoritmos de cálculo tradicionales para el desarrollo del sentido numérico en la Educación Primaria. Recuperado de: http://www.cibem7.semur.edu.uy/7/actas/pdfs/301.pdf.

Butterworth, B., Varma, S., y Laurillard, D. (2011). Dyscalculia: From brain to education. Science, 332(6033), 1049-1053. doi: 10.1016/j.cub.2011.07.005

Díaz-López, Mª. P., Torres, N.M., y Lozano, Mª. C. (2017). Nuevo enfoque en la enseñanza de las matemáticas, el método ABN. International Journal of Developmental and Educational Psychology. INFAD Revista de Psicología, Nº 1-Monográfico 2. Pp: 431-434. doi: 10.17060/ijodaep.2017.n1.v3.1012.

Fletcher, J. M., Lyon, G. R., Fuchs, L. S., y Barnes, M. A. (2007). Learning disabilities: From identification to intervention. Nueva York: Guilford.

García, L., y Quirell, Mª.M. (2017). ¿Hay otra forma de enseñar y aprender matemáticas? Es posible…el método de cálculo abierto ABN. Recuperado de: https://www.actiludis.com/wp-content/uploads/2017/12/ABN-VERSUS-TRADICIONAL.pdf.

Martínez, J. (2011). El método de cálculo abierto basado en números (ABN) como alternativa de futuro respecto a los métodos tradicionales cerrados basados en cifras (CBC). Bordón, Revista de pedagogía, 63(4), 95-110.

Martínez, J. (2012). Desarrollo y mejora de la inteligencia matemática en la Educación Infantil. Madrid: Wolters Kluwer.

Martínez, J., y Sánchez, C. (2013). Resolución de problemas y método ABN. Madrid: Wolters Kluwer.

Quicios, B. (2017, 30 de noviembre). Método ABN para que los pequeños aprendan matemáticas. Guiainfantil. Recuperado el 27 de Abril de 2020 de: https://www.guiainfantil.com/articulos/educacion/aprendizaje/metodo-abn-para-que-los-ninos-aprendan-matematicas/

Ramos, Mª.P. (2005). Las matemáticas a través del juego: aplicaciones prácticas para el aula infantil. Burgos: Fundació Autisme mas casadevall, F.P.

Roman, M. y Murillo, F. J. (2010). Mejorar la calidad de la educación de la primera infancia a través la evaluación. Cuadernos de Educación Infantil 89, 4-6.

Santin, D. y Sicilia, G. (2015). El impacto de la educación infantil en los resultados de primaria: evidencia para España a partir de un experimento natural. En D. Santin et al. (ed.). Reflexiones sobre el sistema educativo español (pp. 45-74). Madrid: Fundación Ramón Areces.

Referencias de imágenes y gráficos

Figura 1. Logo ABN. Recuperado de: https://www.actiludis.com/2016/07/01/comienza-ii-congreso-nacional-calculo-abn/nuevo-logo-abn-color/

Figura 2. Martínez y Sánchez (2011). Bloques para trabajar el ABN.